概率论
| 时间：2013-06-18 | 关注度：169
概率论是研究随机现象数量规律的数学分支。随机现象是相对于决定性现象而言的。在一定条件下必然发生某一结果的现象称为决定性现象。例如在标准大气压下，纯水加热到100℃时水必然会沸腾等。随机现象则是指在基本条件不变的情况下，一系列试验或观察会得到不同结果的现象。每一次试验或观察前，不能肯定会出现哪种结果，呈现出偶然性。例如，掷一硬币，可能出现正面或反面，在同一工艺条件下生产出的灯泡，其寿命长短参差不齐等等。随机现象的实现和对它的观察称为随机试验。随机试验的每一可能结果称为一个基本事件，一个或一组基本事件统称随机事件，或简称事件。
起源
概率论是一门研究事情发生的可能性的学问，但是最初概率论的起源与赌博问题
有关。16世纪，意大利的学者吉罗拉莫·卡尔达诺（Girolam oCardano，1501——1576）开始研究掷骰子等赌博中的一些简单问题。17世纪中叶，当时的法国宫廷贵族里盛行着掷骰子游戏，游戏规则是玩家连续掷 4 次骰子，如果其中没有 6 点出现，玩家赢，如果出现一次 6 点，则庄家（相当于赌场）赢。按照这一游戏规则，从长期来看，庄家扮演赢家的角色，而玩家大部分时间是输家，因为庄家总是要靠此为生的，因此当时人们也就接受了这种现象。
后来为了使游戏更刺激，游戏规则发生了些许变化，玩家这回用 2 个骰子连续掷 24 次，不同时出现2个6点，玩家赢，否则庄家赢。当时人们普遍认为，2 次出现 6 点的概率是一次出现 6 点的概率的 1 / 6 ，因此 6 倍于前一种规则的次数，也既是 24 次赢或输的概率与以前是相等的。然而事实却刚好相反，从长期来看，这回庄家处于输家的状态，于是他们去请教当时的数学家帕斯卡，求助其对这种现象作出解释，这个问题的解决直接推动了概率论的产生。
有人对博弈中的一些问题发生争论，其中的一个问题是“赌金分配问题”，他们决定请教法国数学家帕斯卡（Pascal)和费马（Fermat）基于排列组合方法，研究了一些较复杂的赌博问题，他们解决了分赌注问题、赌徒输光问题。他们对这个问题进行了认真的讨论，花费了3年的思考，并最终解决了这个问题，这个问题的解决直接推动了概率论的产生。 概率与统计的一些概念和简单的方法，早期主要用于赌博和人口统计模型。随着人类的社会实践，人们需要了解各种不确定现象中隐含的必然规律性，并用数学方法研究各种结果出现的可能性大小，从而产生了概率论，并使之逐步发展成一门严谨的学科。概率与统计的方法日益渗透到各个领域，并广泛应用于自然科学、经济学、医学、金融保险甚至人文科学中。
数学家和精算师认为机率是在0至1之间之闭区间的数字，指定给一发生与失败是随机的“事件”。机率P(A)根据机率公理来指定给事件A。一事件A在一事件B确定发生后会发生的机率称为B给之A的条件机率；其数值为
概率
(当P(B)不等于零时)。若B给之A的条件机率和A的机率相同时，则称A和B为独
立事件。且A和B的此一关系为对称的，这可以由一同价叙述：“，当A和B为独立事件时。”中看出。机率论中的两个重要概念为随机变量和随机变量之机率分布这两种概念。 作为数学统计基础的概率论的创始人分别是法国数学家帕斯卡和费马。
概率论
其他对概率论的发展作出重要贡献的人还有荷兰物理、数学家惠更斯，瑞士物理、数学家伯努利，法国数学家美弗，法国数学、天文学家拉普拉斯，德国数学家高斯，法国物理、数学家泊松，意大利数学、医学家卡尔达诺以及苏联数学家柯尔莫哥洛夫。
发展
随着18、19世纪科学的发展，人们注意到在某些生物、物理和社会现象与机会游戏之间有某种相似性，从而由机会游戏起源的概率论被应用到这些领域中；同时这也大大推动了概率论本身的发展。使概率论成为数学的一个分支的奠基人是瑞士数学家j.伯努利，他建立了概率论中第一个极限定理，即伯努利大数定律，阐明了事件的频率稳定于它的概率。随后棣莫弗和p.s.拉普拉斯又导出了第 二个基本极限定理（中心极限定理）的原始
形式。拉普拉斯在系统总结前人工作的基础上写出了《分析的概率理论》，明确给出了概率的古典定义，并在概率论中引入了更有力的分析工具，将概率论推向一个新的发展阶段。19世纪末，俄国数学家p.l.切比雪夫、a.a.马尔可夫、a.m.李亚普诺夫等人用分析方法建立了大数定律及中心极限定理的一般形式，科学地解释了为什么实际中遇到的许多随机变量近似服从正态分布。20世纪初受物理学的刺激，人们开始研究随机过程。这方面a·n·柯尔莫哥洛夫、n.维纳、a·a·马尔可夫、a·r·辛钦、p·莱维及w·费勒等人作了杰出的贡献。
概率论
定义
定义发展史
如何定义概率，如何把概率论建立在严格的逻辑基础上，是概率理论发展的困难所在，对这一问题的探索一直持续了3个世纪。20世纪初完成的勒贝格测度与积分理论及随后发展的抽象测度和积分理论，为概率公理体系的建立奠定了基础。在这种背景下，苏联数学家柯尔莫哥洛夫1933年在他的《概率论基础》一书中第一次给出了概率的测度论的定义和一套严密的公理体系。他的公理化方法成为现代概率论的基础，使概率论成为严谨的数学分支，对概率论的迅速发展起了积极的作用。
公理化定义
设随机实验E的样本空间为Ω。若按照某种方法，对E的每一事件A赋于一个实数P(A)，且满足以下公理：
1°非负性：P(A)≥0；2°规范性：P(Ω)=1；3°可列（完全）可加性：对于两两互不相容的可列无穷多个事件A1，A2，……，An，……，有P(A1∪A2∪……∪An∪……)=P(A1)+P(A2)+……P(An)+……，则称实数P(A)为事件A的概率。
统计定义
设随机事件A在n次重复试验中发生的次数为nA，若当试验次数n很大时，频率nA/n稳定地在某一数值p的附近摆动，且随着试验次数n的增加，其摆动的幅度越来越小，则称数p为随机事件A的概率，记为P(A)=p。
简介
事件的概率则是衡量该事件发生的可能性的量度。虽然在一次随机试验中某
概率论
主要分支有概率空间，随机变量与概率分布，数字特征与特征函数，随机极限理论，随机过程，随机分析，应用概率论，金融数学等。
相关事例
人们普遍认为,对将要发生的机率的一种不好的感觉，或者说不安全感（俗称“点背”）是实际存在的。下面列出的几个例子可以形象阐述人们有时对机率存在的错误的认识：
1.六合彩：在六合彩（49选6）中，一共有13983816种可能性（参阅组合数学），普遍认为，如果每周都买一个不相同的号，最晚可以在13983816/52（周）=268919年后获得头等奖。事实上这种理解是错误的，因为每次中奖的机率是相等的，中奖的可能性并不会因为时间的推移而变大。
概率论
2.生日悖论：在一个足球场上有23个人（2×11个运动员和1个裁判员），不可思议的是，在这23人当中至少有两个人的生日是在同一天的机率要大于50%。
3.轮盘游戏：在游戏中玩家普遍认为，在连续出现多次红色后，出现黑色的机率会越来越大。这种判断也是错误的，即出现黑色的机率每次是相等的，因为球本身并没有“记忆”，它不会意识到以前都发生了什么，其机率始终是18/37。
4.三门问题：在电视台举办的猜隐藏在门后面的汽车的游戏节目中，在参赛者的对面有三扇关闭的门，其中只有一扇门的后面有一辆汽车，其它两扇门后是山羊。游戏规则是，参赛者先选择一扇他认为其后面有汽车的门，但是这扇门仍保持关闭状态，紧接着主持人打开没有被参赛者选择的另外两扇门中后面有山羊的一扇门，这时主持人问参赛者，要不要改变主意，选择另一扇门，以使得赢得汽车的机率更大一些？正确结果是，如果参赛者改变初衷，他的中奖概率将变成2/3。因为打开山羊门的那一刹那，本来的选择结果已经从1/3几率变到了1/2几率，如果改变初衷此时将是1/2中奖的几率。有三种可能的情况，全部都有相等的可能性(1/3)︰参赛者挑山羊一号，主持人挑山羊二号。转换将赢得汽车。参赛者挑山羊二号，主持人挑山羊一号。转换将赢得汽车。参赛者挑汽车，主持人挑两头山羊的任何一头。转换将失败。在头两种情况，参赛者可以通过转换选择而赢得汽车。第三种情况是唯一一种参赛者通过保持原来选择而赢的情况。因为三种情况中有两种是通过转换选择而赢的，所以通过转换选择而赢的概率是2/3。[1]
事件
单位事件、事件空间、随机事件
在一次随机试验中可能发生的唯一的，且相互之间独立的结果被称为单位事件，用e表
概率论
随机事件是事件空间S的子集，它由事件空间S中的单位元素构成，用大写字
概率论
事件的计算
因为事件在一定程度上是以集合的含义定义的，因此可以把集合计算方法直接应用于事件的计算，也就是说，在计算过程中，可以把事件当作集合来对待。
|
A的补集
不属于A的事件发生
|
联集A∪B
或者A或者B或者A，B同时发生
|
交集A∩B
事件A，B同时发生
|
|
差集A\B
不属于B的A事件发生
|
空集A∩B=∅
A，B事件不同时发生
|
子集B⊆A
如A发生，则B也一定发生
|
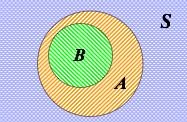
在轮盘游戏中假设A代表事件“球落在红色区域”，B代表事件"球落在黑色
概率论
注意到事件A和B并不是互补的关系，因为在整个事件空间S中还有一个单位事件“零”，其即不是红色也不是黑色，而是绿色，因此A，B的补集应该分别表示如下：
概率
概率
概率的定义
传统概率(拉普拉斯概率)
传统概率的定义是由法国数学家拉普拉斯(Laplace)提出的。如果一
概率论
例如，在一次同时掷一个硬币和一个骰子的随机试验中，假设事件A为获得国徽面且点数大于4，那么事件A的概率应该有如下计算方法：S={(国徽，1点)，(数字，1点)，(国徽，2点)，(数字，2点)，(国徽，3点)，(数字，3点)，(国徽，4点)，(数字，4点)，(国徽，5点)，(数字，5点)，(国徽，6点)
概率论
统计概率
统计概率是建立在频率理论基础上的，分别由英国逻辑学家约翰(JohnVenn1834-1923)和奥地利数学家理查德(RichardVonMises1883-1953)提出，他们认为，获得一个事件的概率值的唯一方法是通过对该事件进行100次，1000次或者甚至10000次的前后相互独立的n次随机试验，针对每次试验均记录下绝对频率值和相对频率值hn(A)，随着试验次数n的增加，会出现如下事实，即相对频率值会趋于稳定，它在一个特定的值上下浮动，也即是说存在着一个极限值P(A)，相对频率值趋向于这个极限值。这个极限值被称为统计概率，表示为：例如，若想知道在一次掷骰子的随机试验中获得6点的概率值可以对其进行3000次前后独立的扔掷试验，在每一次试验后记录下出现6点的次数，然后通过计算相对频率值可以得到趋向于某一个数的统计概率值。
|
扔掷数
|
获得6点的绝对频率
|
获得6点的相对频率
|
|
1
|
1
|
1.00000
|
|
2
|
1
|
0.50000
|
|
3
|
1
|
0.33333
|
|
4
|
1
|
0.25000
|
|
5
|
2
|
0.40000
|
|
10
|
2
|
0.20000
|
|
20
|
5
|
0.25000
|
|
100
|
12
|
0.12000
|
|
200
|
39
|
0.19500
|
|
300
|
46
|
0.15333
|
|
400
|
72
|
0.18000
|
|
500
|
76
|
0.15200
|
|
600
|
102
|
0.17000
|
|
700
|
120
|
0.17143
|
|
1000
|
170
|
0.17000
|
|
2000
|
343
|
0.17150
|
|
3000
|
560
|
0.16867
|
上面提到的这个有关相对频率的经验值又被称为大数定律，是频率理论学家定义概率论的基础。然而没有人可以将骰子无限的扔下去，因此在实践中也就无法有力的证明大数定律，许多来自数学理论的论证至今也没有取得成功。尽管如此，统计概率在今天的实践中具有重要意义，它是数理统计的基础。
概率公理
如果一个函数P指定给每一个事件空间S中的事件A一个实数P(A)，并且其满足下面的3个公理，那么函数P叫做概率函数，相应的P(A)叫做事件A的概率。
|
公理1：
事件A的概率P(A)是一个非负实数。
公理2：
完全事件的概率值为1。
公理3：P（A+B)=P(A)+P(B)，如果A∩B=0
空集事件的加法法则。
|
不难看出，上述公理适用于包括拉普拉斯概率和统计概率在内的所有概率定义。如果若干事件间的关系是两两空集，那么公理3还可以扩展为如下形式：
公理3：P(A∪B∪C∪…）=P(A)+P(B)+P(C)+…
概率
计算
需要提及的是下面将要介绍的9个计算概率的定理与上面已经提及的事件的计算没有关系，所有关于概率的定理均由概率的3个公理得来，同时适用于包括拉普拉斯概率和统计概率在内的所有概率理论。
定理1
(互补法则)
与A互补事件的概率始终是1-P(A)
证明：
事件A和ā是互补关系，由公理3和公理2可得
利用互补法则，可以解决下面这个问题，在两次连续旋转的轮盘游戏中，至少有一次是红色的概率是多少？
第一次旋转红色不出现的概率是19/37，按照乘法法则，第二次也不出现红色的概率是(19/37)2=0.2637，因此在这里互补概率就是指在两次连续旋转中至少有一次是红色的概率，
定理2
不可能事件的概率为零：证明： Q和S是互补事件，按照公理2有
P(S)=1，再根据上面的定理1得到P(Q)=0
定理3
如果若干事件A1，A2，...An∈S每两两之间是空集关系，那么这些所有事件集合的概率等于单个事件的概率的和。
注意针对这一定理有效性的决定因素是A1...An事件不能同时发生（为互斥事件）。例如，在一次掷骰子中，得到5点或者6点的概率是： P=P(A5)+P(A6)
定理4
如果事件A，B是差集关系，则有P（A-B）=P（A~B），
证明：事件A由下面两个事件组成：和由公理3得，
定理5
(任意事件加法法则)
对于事件空间S中的任意两个事件A和B，有如下定理： 概率
证明：
事件A∪B由下面三个事件组成：首先根据定理4有：再根据定理3得：
例如，在由一共32张牌构成的斯卡特扑克牌中随机抽出一张，其或者是"方片"或者是""的概率是多少？
事件A，B是或者的关系，且可同时发生，就是说抽出的这张牌即可以是"方片"，又可以是""，A∩B(既发生A又发生B)的值是1/32，(从示意图上也可以看出，即是方片又是只有一张，即概率是1/32)，因此有如下结果：
从图片上也可看出，符合这一条件的恰好是11张牌。注意到定理3是定理5的特殊情况，即A，B不同时发生，相应的P(A∩B)=0。
定理6
(乘法法则) 事件A，B同时发生的概率是：
轮盘游戏示意图
注意应用如上公式的前提是事件A，B相互之间有一定联系，公式中的P(A|B)是指在B条件下A发生的概率，又称作条件概率。回到上面的斯卡特游戏中，在32张牌中随机抽出一张，即是方片又是A的概率是多少呢？现用P(A)代表抽出方片的概率，用P(B)代表抽出A的概率，很明显，A，B之间有一定联系，即A里包含有B，B里又包含有A，在A的条件下发生B的概率是P(B|A)=1/8，则有：
或者，
从上面的图中也可以看出，符合条件的只有一张牌，即方片A。
另一个例子，在32张斯卡特牌里连续抽两张(第一次抽出的牌不放回去)，连续得到两个A的概率是多少呢？
设A，B分别为连续发生的这两次事件，人们看到，A，B之间有一定联系，即B的概率由于A发生了变化，属于条件概率，按照公式有：
定理7
(无关事件乘法法则)
两个不相关联的事件A，B同时发生的概率是：注意到这个定理实际上是定理6(乘法法则)的特殊情况，如果事件A，B没有联系，则有P(A|B)=P(A)，以及P(B|A)=P(B)。观察一下轮盘游戏中两次连续的旋转过程，P(A)代表第一次出现红色的概率，P(B)代表第二次出现红色的概率，可以看出，A与B没有关联，利用上面提到的公式，连续两次出现红色的概率为：
忽视这一定理是造成许多玩家失败的根源，普遍认为，经过连续出现若干次红色后，黑色出现的概率会越来越大，事实上两种颜色每次出现的概率是相等的，之前出现的红色与之后出现的黑色之间没有任何联系，因为球本身并没有"记忆"，它并不"知道"以前都发生了什么。同理，连续10次出现红色的概率为P=(18/37)10=0.0007
完全概率
n个事件H1，H2，...Hn互相间独立，且共同组成整个事件空间S，即
，以
这时A的概率可以表示为，证明：
概率
按照公理3，有根据乘法法则，因此有，
例如，一个随机试验工具由一个骰子和一个柜子中的三个抽屉组成，抽屉1里有14个白球和6个黑球，抽屉2里有2个白球和8个黑球，抽屉3里有3个白球和7个黑球，试验规则是首先掷骰子，如果获得小于4点，则抽屉1被选择，如果获得4点或者5点，则抽屉2被选择，其他情况选择抽屉3。然后在选择的抽屉里随机抽出一个球，最后抽出的这个球是白球的概率是：
P(白)=P(白|抽1)·P(抽1)+P(白|抽2)·P(抽2)+P(白|抽3)·P(抽3)
=(14/20)·(3/6)+(2/10)·(2/6)+(3/10)·(1/6)
=28/60=0.4667
从例子中可看出，完全概率特别适合于分析具有多层结构的随机试验的情况。
贝叶斯定理
贝叶斯定理由英国数学家贝叶斯(ThomasBayes1702-1761)发展，用来描述两个条件概率之间的关系，比如P(A|B)和P(B|A)。按照定理6的乘法法则，P(A∩B)=P(A)·P(B|A)=P(B)·P(A|B)，可以立刻导出贝叶斯定理：如上公式也可变形为例如：一座别墅在过去的20年里一共发生过2次被盗，别墅的主人有一条狗，狗平均每周晚上叫3次，在盗贼入侵时狗叫的概率被估计为0.9，问题是：在狗叫的时候发生入侵的概率是多少？
人们假设A事件为狗在晚上叫，B为盗贼入侵，则P(A)=3/7，P(B)=2/(20·365)=2/7300，P(A|B)=0.9，按照公式很容易得出结果：另一个例子，现分别有A，B两个容器，在容器A里分别有7个红球和3个白球，在容器B里有1个红球和9个白球，现已知从这两个容器里任意抽出了一个球，且是红球，问这个红球是来自容器A的概率是多少?
假设已经抽出红球为事件B，从容器A里抽出球为事件A，则有：P(B)=8/20，P(A)=1/2，P(B|A)=7/10，按照公式，则有：应用
虽然概率论最早产生于17世纪，然而其公理体系只在20世纪的20至30年代才建立起来并得到迅速发展，在过去的半个世纪里概率论在越来越多的新兴领域显示了它的应用性和实用性，例如：物理、化学、生物、医学、心理学、社会学、政治学、教育学，经济学以及几乎所有的工程学等领域。特别值得一提的是，概率论是今天数理统计的基础，其结果被用做问卷调查的分析资料或者对经济前景进行预测
- 文章作者：百家乐
- 本文网址：http://www.ikepu.com/datebase/briefing/maths/probability_theory.htm
- Tags：